Что такое «супергидрофильные поверхности» и как их можно охарактеризовать используя мнимый краевой угол?

Значение краевого угла смачивания (КУС) воды на твёрдой поверхности является важной характеристикой смачиваемости поверхности. На основе величины КУС были определены различные типы смачиваемости, такие как супергидрофильность, гидрофильность, гидрофобность и супергидрофобность (Рис. 1). Наименьшее значение КУС, равное 0^o, достигается при полном растекании капли воды на твёрдой поверхности.

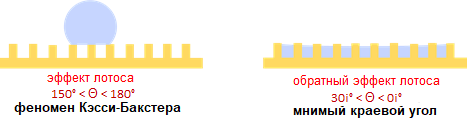
Как различаются между собой материалы, на которых капля воды растекается полностью? Существуют материалы у которых значение КУС ниже 0^o и как отличить эти материалы друг от друга?

Различить супергидрофильные материалы с КУС равным 0^o возможно на основе анализа значения мнимого краевого угла.

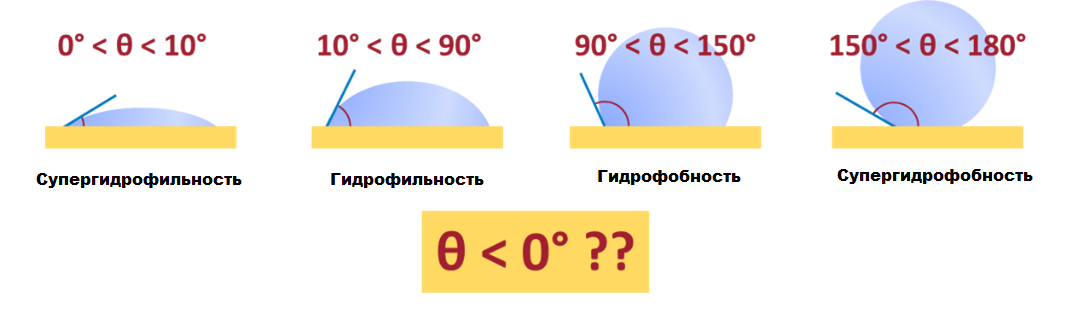
Рис. 1 Классификация поверхностей по их характеристикам смачиваемости

Логично что значение КУС равное 0^o является пределом для классического анализа краевого угла оптическим методом. Альтернативным методом измерения КУС является динамический анализ с помощью тензиометра. Для проведения измерения образец закрепляется в фиксатор, соединённый с весовой ячейкой и погружается в воду. Если поверхность образца гидрофильная, контакт образца с водой приводит к растеканию воды по его поверхности, а прибор зарегистрирует набор массы образца за некоторый промежуток времени. При изучении различных материалов, группа Jennissen et al. получила первые свидетельства того, что при полном смачивании супергидрофильных шероховатых поверхностей типа титановых сплавов с плазменным напылением на значение КУС действуют дополнительные силы. Рассчитанные значения КУС лежали ниже 0^o и получили наименование мнимого краевого угла с обозначением Q.

При анализе супергидрофильных материалов весовая ячейка тензиометра в дополнение к стандартной для такого анализа силе Вильгельми F_W регистрирует дополнительную силу F_Σ,, вызванную растеканием воды по поверхности образца, и капиллярную силу (см. уравнение 1; где P – периметр смачивания, γ – поверхностное натяжение, κ – константа, F_imb – сила, обусловленная задержкой воды в неровностях поверхности образца). Эта дополнительная сила может привести к значению cos q 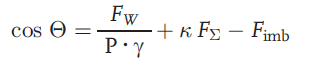> 1.

(1)

Если супергидрофильные материалы анализировать с помощью классических методов, то оперируя только рациональными числами невозможно решить вышеуказанное уравнение для cos q > 1, поэтому классический весовой метод даёт значение краевого угла равного нулю, для cos q ≥ 1 (Рис. 2A). Кривая значений краевого угла не охватывает ту часть кривой весовых значений, которая при расчёте будет давать cos q > 1. Новый расчётный метод вводит понятие мнимого краевого угла, что даёт возможность построения кривой краевых углов для cos q > 1 и продолжения её из области мнимых чисел в область рациональных чисел (Рис. 2Б). Таким образом, возможно рассчитать значения краевого угла для cos q ≥ 1 и экстраполировать до нуля глубину погружения образца для получения значения растущего мнимого краевого угла Q = 20.6i° для титано-плазменного напыления TPS. На графике 2В отражено, что супергидрофильные поверхности показывают экстремально высокую скорость смачивания.

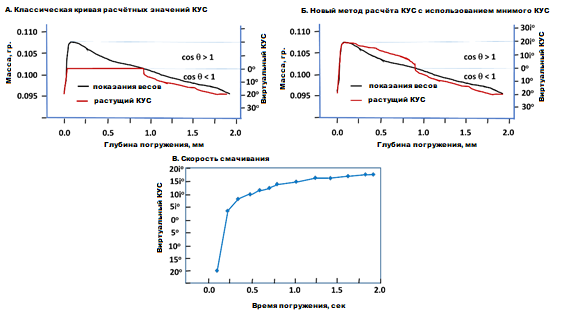
Рис. 2 A) и Б) чёрная линия: исходный график весовых значений (реальные значения массы образца). Красная линия: виртуальные значения КУС для всех измеренных значений массы, рассчитанные в соответствии с Q = arccos (F/Pg) с силой F, включающей в себя силы F_W и F_Σ  В) Скорость смачивания супергидрофильной поверхности с титано-плазменным напылением, рассчитанная из  исходных данных весовой ячейки.

Что приводит к возникновению дополнительной силы и, как следствие, к измерению мнимого краевого угла? Эффект смачиваемости шероховатых поверхностей базируется на четырёх физических явлениях: когезии, адгезии, растекании и погружении. От этих четырёх феноменов зависит появление дополнительной силы и мнимого краевого угла на шероховатых поверхностях. Для поверхностей с титано-плазменным напылением принимаем, что капиллярные явления на пористых поверхностях могут привести к возникновению дополнительных сил, ответственных за мнимый краевой угол. На рисунке 2В погружение в воду 10,4-миллиметровой пластинки с титано-плазменным напылением на глубину 7–8 мкм (1/1351 от 10.4 мм) даёт мнимый краевой угол величиной в 10i^o, что свидетельствует о моментальном смачивании сухой пластинки образца. Этот эффект может быть проиллюстрирован с помощью капиллярных сил, ведущих к менискозависимому заполнению неровностей на поверхности образца. Плёнка воды поднимается вверх по пластинке от смоченного нижнего края образца в сторону сухой его поверхности, то есть, наблюдается растекание первичной плёнки воды до полного идеального смачивания шероховатой поверхности образца (Рис. 3Б).

Рис. 3 Модель неравновесного состояния мениска зависимого от заполнения шероховатостей до полного смачивания шероховатой поверхности.

Расчёт мнимого краевого угла даёт возможность различать между собой супергидрофильные поверхности, дающие при классическом анализе значение КУС, равное нулю. Феномен супергидрофильности играет важную роль при изготовлении материалов для протезирования, так как для этих материалов важна биосовместимость с организмом человека.

Компания DataPhysics Instruments является единственным производителем тензиометров, в программное обеспечение которых встроен метод мнимого краевого угла. Это делает нашу серию тензиометров DCAT идеальным оборудованием для исследований гидрофильных материалов, так как позволяет количественно рассчитать разницу между материалов с полной смачиваемостью путём расчёта мнимого краевого угла.

Для получения более детальной информации о расчёте мнимого краевого угла на тензиометрах серии DCAT компании DataPhysics Instruments обращайтесь к нам.

Полная статья по теме:

Hyperhydrophilic rough surfaces and imaginary contact angles; H. P. Jennissen; Mat. -wiss. u.Werkstofftech. 2012, 43, 743-750; DOI: 10.1002/mawe.201200961